Vídeo novo!!! : 

Postado por : Camila Carvalho, alunda da EEEP Dep. Jose Walfrido Monteiro.

Hiparco de Nicéia viveu no século II a.C. e é considerado o mais eminente dos astrônomos da Antiguidade. Cuidadoso ele desenvolveu importantes trabalhos no observatório de Rodes. Creditam-se a ele feitos como a determinação do mês lunar médio, um cálculo de inclinação do plano da órbita da terrestre e a organização de um catálogo estelar. A Trigonometria da época era baseada na relação entre um arco arbitrário e sua corda. Os estudos de Hiparco sobre o cálculo do comprimento das cordas deram origem a primeira tabela trigonométrica. Apesar de a corda de um arco não ser o seno, uma vez conhecido o valor de seu comprimento, pode-se calcular o seno da metade do arco. Veja na figura abaixo como podemos calcular o seno a partir do comprimento da corda:

Acredita-se que uma tábua de cordas posterior foi desenvolvida pelo matemático Claudio
Ptolomeu (85 a 165 d.C.) a partir da descoberta de Hiparco.

 Fonte : Livro "A conquista da Matemática."

Por : Lygia Fernandes Angelim. Agronegócio - 1 ano.

Função

Uma função é dada por uma relação entre dois conjuntos, definida por uma lei de formação. Ao estudarmos uma função determinamos o domínio, o contradomínio e a imagem. Vamos através de diagramas de flechasdemonstrar esses três elementos pertencentes ao estudo das funções.

Os elementos do conjunto A serão relacionados com os elementos do conjunto B através de uma lei de formação. Observe:

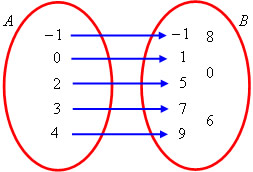
O conjunto A é formado pelos elementos {–1, 0, 2, 3, 4} e o conjunto B pelos elementos {–1, 0, 1, 5, 6, 7, 8, 9}. Observe que os elementos do conjunto A se relacionam com os elementos de B segundo a função de A → B (função de A em B) pela lei de formação f(x) = 2x + 1. Observe:

f(–1) = 2 * (–1) + 1 = –2 + 1 = –1
f(0) = 2 * 0 + 1 = 0 + 1 = 1
f(2) = 2 * 2 + 1 = 4 + 1 = 5
f(3) = 2 * 3 + 1 = 6 + 1 = 7
f(4) = 2 * 4 + 1 = 8 + 1 = 9 

Nessa relação, temos que o domínio é dado pelo conjunto A, o contradomínio representado pelo conjunto B e a imagem pelos elementos de B que possuem relação com os elementos do conjunto A.

Domínio: {–1, 0, 2, 3, 4}
Contradomínio: {–1, 0, 1, 5, 6, 7, 8, 9}
Imagem: {–1, 1, 5, 7, 9}


Na seguinte situação, relacionaremos o conjunto A com o conjunto B, obedecendo a uma nova lei de formação, dada por   f(x) = x² – 2. Observe os cálculos que determinarão o conjunto imagem dos elementos de A.

f(–1) = (–1)² – 2 = 1 – 2 = –1
f(0) = 0² – 2 = 0 – 2 = –2
f(2) = 2² – 2 = 4 – 2 = 2
f(3) = 3² – 2 = 9 – 2 = 7
f(4) = 4² – 2 = 16 – 2 = 14

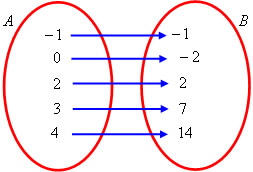
Domínio: {–1, 0, 2, 3, 4}
Contradomínio: {–2, –1, 2, 7, 14}
Imagem: {–2, –1, 2, 7, 14}

Em algumas situações o contradomínio e a imagem são iguais, isto é, possuem os mesmos elementos.


Na seguinte relação, a lei de formação será dada por f(x) = x³, o conjunto A será formado pelos elementos {–2, –1, 0, 1, 2, 3}. Vamos determinar o conjunto B imagem desse domínio representado pelo conjunto A.

f(–2) = (–2)³ = –8
f(–1) = (–1)³ = –1
f(0) = 0³ = 0
f(1) = 1³ = 1
f(2) = 2³ = 8
f(3) = 3³ = 27

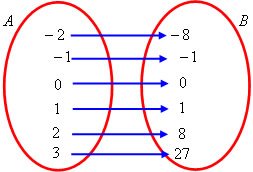
Domínio: {–2, –1, 0, 1, 2, 3}
Contradomínio: {–8, –1, 0, 1, 8, 27}
Imagem: {–8, –1, 0, 1, 8, 27}

Por Marcos Noé

Via Francielly Dias (Furakao), aluna da EEEP Dep. Jose walfrido Monteiro

ola eu liliane mota vou mostra pra vcs o conteudo do mes das provas.......

http://www.seduc.ce.gov.b

ola essa e uma postagem de um diograma de flexas curtam air muito massa estudar funçao .....

valeu a todos que curtiram nosso bogg

liliane mota pinheiro........

bom dia

MIL CAIRAO AO TEU LADO DEZ MIL A TUA DIREITA MAIS TU NAO SERAS ATINGIDO

QUE HOJE O SENHO POSSA LIVRAR TODOS NOIS DE TODOS OS MAL AMEM

LILIANE MOTA PINHEIRO

Aqui no blog já foram postados vários vídeos sobre trigonometria do triângulo retângulo, e nunca foi postado um sobre função.
Hoje, eu (Bruno Weiman), irei disponibilizar para vocês os melhores vídeos que eu encontrei.
Confiram :

Postado por : Bruno Weiman Dias Siqueira, aluno da EEEP Dep. Jose Walfrido Monteiro.

Muita gente fala de Plano Cartesiano, mas nem todos sabem exatamente o que é. Por isso eu, Filipe Leandro, estou fazendo esta postagem. O Plano Cartesiano foi criado pelo matemático René Descartes. Como ele associava a geometria à álgebra, esta foi a forma que ele criou para representar graficamente expressões algébricas.

A sua utilização mais simples é a de representarmos graficamente a localização de pontos em um determinado plano. Através dele também podemos representar um segmento de reta ou um triângulo, por exemplo.

O plano cartesiano é composto de duas retas perpendiculares e orientadas, uma horizontal e outra vertical.

Damos no nome de eixo x ou eixo das abscissas à reta horizontal. À vertical denominamos de eixo y ou eixo das ordenadas.

A orientação positiva das retas é representa por uma seta como podemos ver na figura mais abaixo.

Postado por : Filipe Leandro, aluno da EEEP.. Dep. José Walfrido Monteiro.

Oi, sou a Tainá , e hoje vou mostrar para vocês algumas imagens do conteúdo desse mês para fixar.

Domínio é um sinônimo para conjunto de saída, ou seja, para esta função o domínio é o próprio conjunto X.

Este subconjunto (Y) é chamado de conjunto imagem, e é composto por todos os elementos em que as flechas de relacionamento chegam.

Postado por Tainá Martins, aluna da EEEP Dep. José Walfrido Monteiro.

Preparamos um pequeno vídeo para melhor compreensão da matéria ^^ Deem uma olhada :

Compartilhem com seus amigos e colegas :)

Por : Camila Carvalho

Liliane Mota

Filipe Leandro

Bruno Weiman

Tainá Martins

Postado por Bruno Weiman, aluno da EEEP Dep. José Walfrido Monteiro.

Postado por : Filipe Leandro, aluno da EEEP José Walfrido Monteiro.

Olá gatinhos e gatinhas mecânicos! Hoje a Camila e eu,Liliane, trouxemos para vocês um vídeo divertidíssimo e criativo, feito pelas gatinhas lá da Bahia. Confiram:

É isso aí, mecânicos. Nesse blog nós estamos constantemente mostrando como pode ser divertido aprender fórmulas e cálculos, basta dedicação. Acham que acabou? Não viram nem a metade!
Esses nerds hoje em dia estão cada vez mais "tops" e descomplicam nossa vida que é uma beleza. É tanto que nem precisa entender a língua inglesa para compreender a mensagem dos vídeos a seguir. De qualquer forma, vale a pena conferir o trabalho dos caras :

Bons estudos pessoal!
Postado por :Liliane Mota e Camila Carvalho.

Regrinhas para decorar as fórmulas

Pois é ,pessoal. As provas e trabalhos chegam, e fica aquela dúvida na cabeça de como vamos conseguir decorar todas aquelas fórmulas. Pensando nisso, pesquisei bastante na internet e achei algumas coisinhas que podem ajudar na hora da "decoreba" ;D

Razões Trigonométricas no Triângulo Retângulo

Foram tiradas de uma ilha havaiana chamadas SOH CAH TOA

Seno = Oposto/Hipotenusa

Cosseno = Adjacente/Hipotenusa

Tangente = Oposto/Adjacente

Usando o cosseno faz um funk: coça coça, senta senta

cos(A+B) = cosAcosB – senAsenB

cos(A-B) = cosAcosB + senAsenB

O seno é mais culto, curte uma literatura:
“Minha terra tem palmeiras, onde canta o sabiá, senoA cossenoB, senoB cossenoA”

sen(A+B) = senAcosB + senBcosA

sen(A-B) = senAcosB – senBcosA

Preste atenção com os sinais!

Fórmula fundamental da trigonometria

Enterro de dois anões num, junta os dois quadrados que dá um.

sen²x + cos²x  = 1

Comprimento da circunferência

Quem descobriu foram dois franceses chamados Pierre

C = 2.pi.R

A trigonometria que para muitos parece ser um "bicho de 7 cabeças", pode se tornar mais fácil se tivermos um macete para decorar as fórmulas básicas
Anexei abaixo uma imagem que pode nos ajudar.
Basta decorar a palavra SOCATOA sobre as letra HH AO

Para melhor compreensão do que foi citado acima, veja esse vídeo : 

Postado por: Camila Carvalho, aluna da EEEP Dep. José Walfrido Monteiro

Olá estudantes ^^ Hoje disponibilizaremos alguns vídeos para os ajudarem a revisar provas e trabalhos

Bons estudos e até a próxima aula!

Postado por: Camila Carvalho, aluna da EEEP Dep. José Walfrido Monteiro

Introduzimos aqui alguns conceitos relacionados com a Trigonometria no triângulo retângulo, assunto comum na oitava série do Ensino Fundamental. Também dispomos de uma página mais aprofundada sobre o assunto tratado no âmbito do Ensino Médio.

A trigonometria possui uma infinidade de aplicações práticas. Desde a antiguidade já se usava da trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns.

Algumas aplicações da trigonometria são:

• Determinação da altura de um certo prédio.
  
• Os gregos determinaram a medida do raio de terra, por um processo muito simples.
• Seria impossível se medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
• Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
• Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.

Tudo isto é possível calcular com o uso da trigonometria do triângulo retângulo.

Triângulo Retângulo

É um triângulo que possui um ângulo reto, isto é, um dos seus ângulos mede noventa graus, daí o nome triângulo retângulo. Como a soma das medidas dos ângulos internos de um triângulo é igual a 180°, então os outros dois ângulos medirão 90°.

Observação: Se a soma de dois ângulos mede 90°, estes ângulos são denominados complementares, portanto podemos dizer que o triângulo retângulo possui dois ângulos complementares.

Para ver mais detalhes sobre triângulos clique aqui.

Lados de um triângulo retângulo

Os lados de um triângulo retângulo recebem nomes especiais. Estes nomes são dados de acordo com a posição em relação ao ângulo reto. O lado oposto ao ângulo reto é a hipotenusa. Os lados que formam o ângulo reto (adjacentes a ele) são os catetos.

Termo	Origem da palavra
Cateto	Cathetós: (perpendicular)
Hipotenusa	Hypoteinusa: Hypó(por baixo) + teino(eu estendo)

Para padronizar o estudo da Trigonometria, adotaremos as seguintes notações:

Letra	Lado	Triângulo	Vértice = Ângulo	Medida
a	Hipotenusa		A = Ângulo reto	A=90°
b	Cateto		B = Ângulo agudo	B<90°
c	Cateto		C = Ângulo agudo	C<90°

Para ver mais detalhes sobre ângulos clique aqui.

Nomenclatura dos catetos

Os catetos recebem nomes especiais de acordo com a sua posição em relação ao ângulo sob análise. Se estivermos operando com o ângulo C, então o lado oposto, indicado por c, é o cateto oposto ao ângulo C e o lado adjacente ao ângulo C, indicado por b, é o cateto adjacente ao ângulo C.

Ângulo	Lado oposto	Lado adjacente
C	c cateto oposto	b cateto adjacente
B	b cateto oposto	c cateto adjacente

Um dos objetivos da trigonometria é mostrar a utilidade do conceitos matemáticos no nosso cotidiano. Iniciaremos estudando as propriedades geométricas e trigonométricas no triângulo retângulo. O estudo da trigonometria é extenso e minucioso.

Propriedades do triângulo retângulo

1. Ângulos: Um triângulo retângulo possui um ângulo reto e dois ângulos agudos complementares.
2. Lados: Um triângulo retângulo é formado por três lados, uma hipotenusa (lado maior) e outros dois lados que são os catetos.
3. Altura: A altura de um triângulo é um segmento que tem uma extremidade num vértice e a outra extremidade no lado oposto ao vértice, sendo que este segmento é perpendicular ao lado oposto ao vértice. Existem 3 alturas no triângulo retângulo, sendo que duas delas são os catetos. A outra altura (ver gráfico acima) é obtida tomando a base como a hipotenusa, a altura relativa a este lado será o segmento AD, denotado por h e perpendicular à base.
   

A hipotenusa como base de um triângulo retângulo

Tomando informações da mesma figura acima, obtemos:

1. o segmento AD, denotado por h, é a altura relativa à hipotenusa CB, indicada por a.
2. o segmento BD, denotado por m, é a projeção ortogonal do cateto c sobre a hipotenusa CB, indicada por a.
3. o segmento DC, denotado por n, é a projeção ortogonal do cateto b sobre a hipotenusa CB, indicada por a.

Projeções de segmentos

Introduziremos algumas idéias básicas sobre projeção. Já mostramos, no início deste trabalho, que a luz do Sol ao incidir sobre um prédio, determina uma sombra que é a projeção oblíqua do prédio sobre o solo.

Tomando alguns segmentos de reta e uma reta não coincidentes é possível obter as projeções destes segmentos sobre a reta.

Nas quatro situações apresentadas, as projeções dos segmentos AB são indicadas por A'B', sendo que no último caso A'=B' é um ponto.

Projeções no triângulo retângulo

Agora iremos indicar as projeções dos catetos no triângulo retângulo.

1. m = projeção de c sobre a hipotenusa.
2. n = projeção de b sobre a hipotenusa.
3. a = m+n.
4. h = média geométrica entre m e n. Para saber mais, clique sobre média geométrica.

Relações Métricas no triângulo retângulo

Para extrair algumas propriedades, faremos a decomposição do triângulo retângulo ABC em dois triângulos retângulos menores: ACD e ADB. Dessa forma, o ângulo A será decomposto na soma dos ângulos CÂD=B e DÂB=C.

Observamos que os triângulos retângulos ABC, ADC e ADB são semelhantes.

Triângulo	hipotenusa	cateto maior	cateto menor
ABC	a	b	c
ADC	b	n	h
ADB	c	h	m

Assim:

a/b = b/n = c/h
a/c = b/h = c/m
b/c = n/h = h/m

logo:

a/c = c/m    equivale a    c² = a.m
a/b = b/n    equivale a    b² = a.n
a/c = b/h    equivale a    a.h = b.c
h/m = n/h    equivale a    h² = m.n

Existem também outras relações do triângulo inicial ABC. Como a=m+n, somando c² com b², obtemos:

c² + b² = a.m + a.n = a.(m+n) = a.a = a²

que resulta no Teorema de Pitágoras:

a² = b² + c²

A demonstração acima, é uma das várias demonstrações do Teorema de Pitágoras.

Essa introdução vale como uma revisão do conteúdo passado.

^^ Até a próxima aula
Fonte : http://pessoal.sercomtel.com.br/